Exercice 4
La partie mécanique d’un haut-parleur électrodynamique est constitué d’une membrane mobile, solidaire d’un cylindre creux sur lequel est enroulé le fil d’une bobine de cuivre. L’ensemble, appelé équipage mobile (S) possède une masse totale m et s’astreint à se déplacer selon l’axe x’x. La suspension est modélisée par un ressort de constante de raideur k, de longueur à vide l0, pouvant travailler en extension comme en compression.
Le système (S) peut coulisser sans frottement sur une tige horizontale fixée sur un bâti vertical.
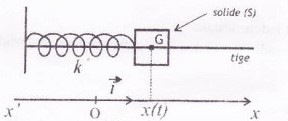
On écarte le solide (S) de sa position d’équilibre x0 à un instant qu’on prend comme origine des dates puis on l’abandonne sans vitesse initiale.
1. En application la deuxième loi de Newton, établir l’équation différentielle du mouvement du solide (S).
2. Vérifier que x(t)=x0 sin(ωt + φ) où x0, ω et φ sont des constantes, est une solution de l’équation différentielle.
3. Etablir l’expression de l’énergie mécanique du système { solide (S) + ressort + Terre} en fonction de x, v, k et m, et montrer que cette énergie mécanique peut s’écrire en fonction de k et x0. Conclure.