Présentation d’une méthode : étude d’un hangar (html)
Exercice sur les treillis plans
Niveau: BAC PRO BEP
OBJECTIF : dimensionner la section des barres constituant ce hangar
On donne :
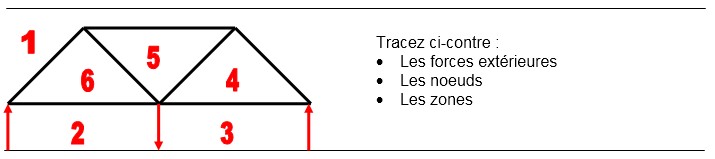
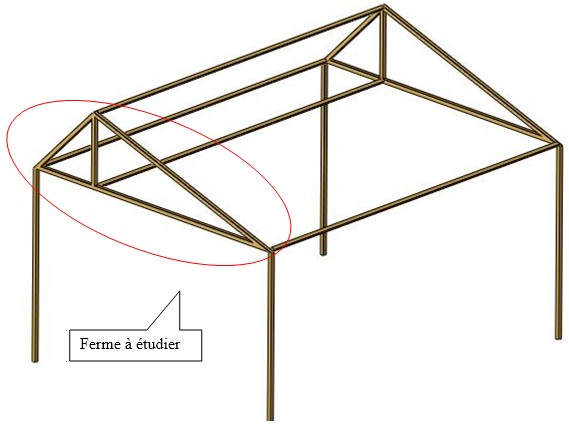
Le schéma constitutif du hangar
On demande :
(pour la ferme entourée ci-dessous)
- La nature des sollicitations dans les barres
- La valeur des efforts dans ces barres
RAPPEL DE STATIQUE
Lorsqu’un système en équilibre est soumis à l’action de 2 forces : celles-ci sont opposées
Il y a 2 cas possibles:

LES TREILLIS PLANS ou SYSTÈMES TRIANGULÉS
DÉFINITIONS
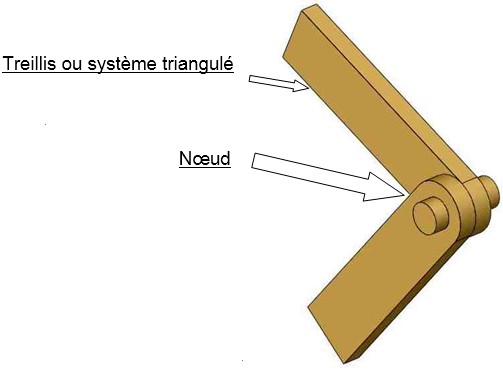
Treillis ou système triangulé :
Assemblage de barres rectilignes formant entre elles des triangles
Nœud :
Point de rencontre de plusieurs barres
HYPOTHÈSES
- assemblages géométriquement invariables
- forces coplanaires
- poids des barres négligés
- nœuds équivalents à des liaisons pivot sans frottement
- forces extérieures appliquées sur les nœuds
- barres soumises à traction ou compression
RELATION NOEUDS-BARRES
![]()
Si b>2n-3 : trop de liaisons, système hyperstatique àcontraintes internes
Si b<2n-3 : système non rigide, mobilité des barres
b=2n-3 : système statiquement déterminé ou isostatique
EXEMPLES :
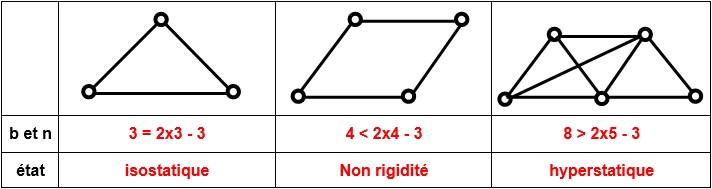
![]()
Si la structure repose sur des appuis encastrés :
EXEMPLES :
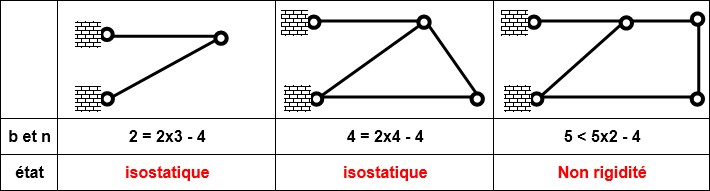
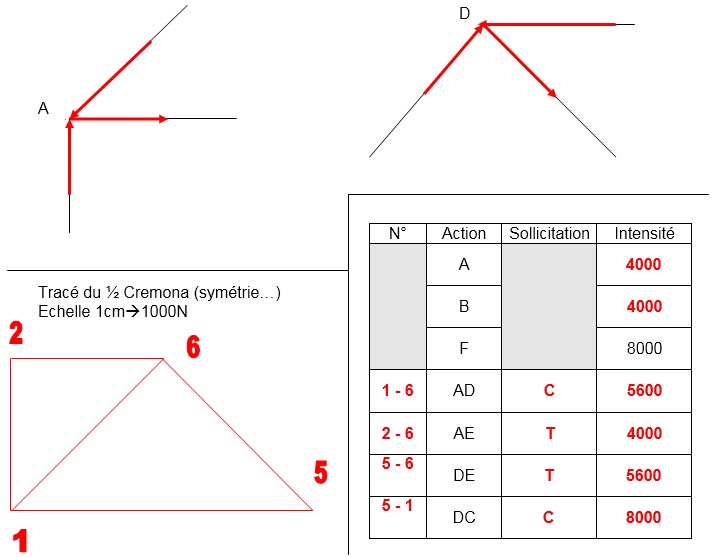
MÉTHODE DE CREMONA
Elle permet de déterminer les efforts dans toutes les barres d’une structure en rassemblant sur un seul dynamique tous les polygones des forces équilibrant chaque nœud.
Appliquons cette méthode à notre structure :
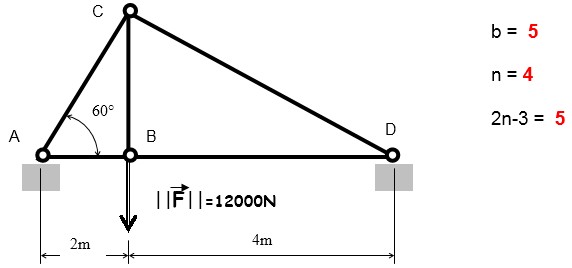
1- CALCUL DES ACTIONS AUX APPUIS
Le système étant en équilibre :
La somme des moments en A doit être nulle:
- (12000x2) + (Dx8) =0 et donc D=+3000N
![]()
La somme des forces extérieures appliquées sur la structure doit être nulle :
A+D-F=0 et donc A = F - D = 12000 – 3000 = +9000
![]()
2- TRACÉ DES RÉGIONS
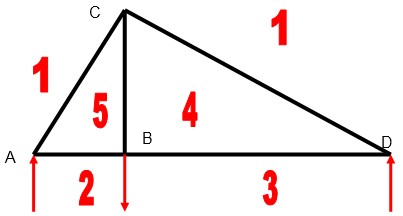
Elles sont limitées par des frontières :
- les forces extérieures
- les barres
UTILISATION :
- On étudie les nœuds un par un
- On tourne dans le sens trigo
- Chaque frontière correspond à une action.
3- ÉQUILIBRE DES NŒUDS
On ne peut réaliser l’équilibre d’un nœud que s’il se trouve à l’intersection de 2 barres dont les efforts sont inconnus. Le nœud C étant situé à l’intersection de 3 barres ne peut être réalisé en premier.
Le nœud A est en équilibre sous l’action de 3 forces :
La frontière 1-2 correspond à la réaction A exercée par l’appui
La frontière 2-5 correspond à la force (inconnue) exercée par la barre AB sur le nœud A
La frontière 5-1 correspond à la force (inconnue) exercée par la barre AC sur le nœud A
Choix de l’ordre des nœuds à équilibrer : A, B, C et D (voit tableau ci-dessous)
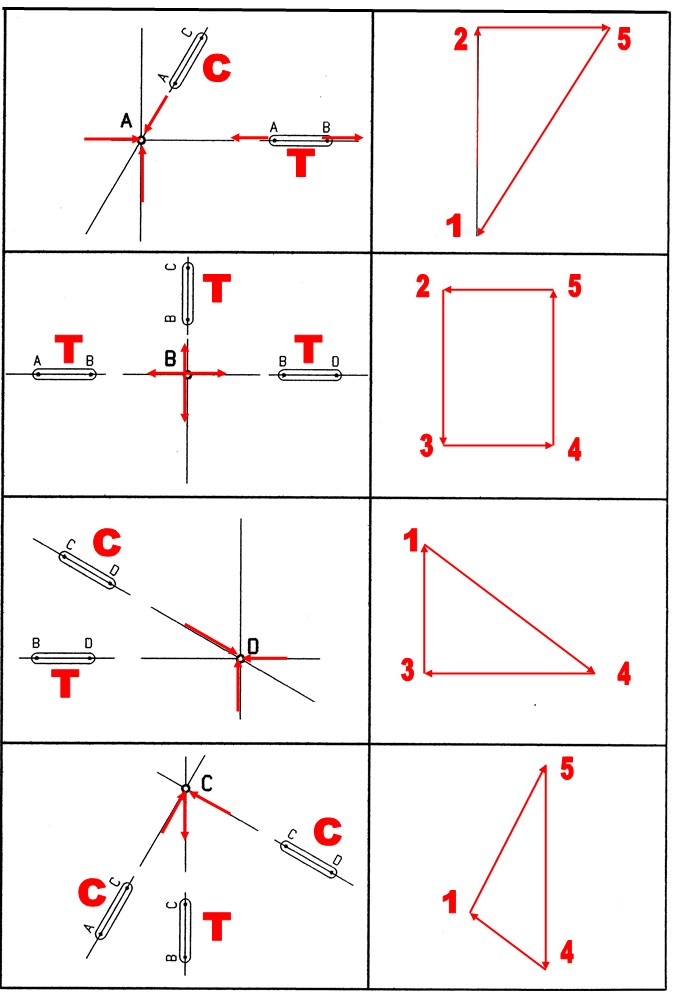
TRACÉ DU CREMONA
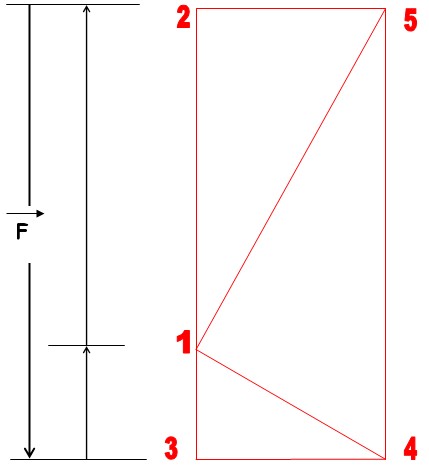
|
Actions |
Désignation sur graphe |
Sens de l’action sur le nœud |
Sollicitation dans la barre |
Intensité en N |
|
A |
1 - 2 |
|
|
9000 |
|
D |
3 - 1 |
3000 |
||
|
F |
2 - 3 |
12000 |
||
|
Barre AB sur noeud A |
2 - 5 |
A vers B |
T |
5200 |
|
Barre AB sur noeud B |
B vers A |
|||
|
Barre BD sur noeud B |
3 - 4 |
B vers D |
T |
5200 |
|
Barre BD sur noeud D |
D vers B |
|||
|
Barre DC sur noeud D |
1 - 4 |
C vers D |
C |
6000 |
|
Barre DC sur noeud C |
D vers C |
|||
|
Barre AC sur noeud A |
1 - 5 |
C vers A |
C |
10400 |
|
Barre AC sur noeud C |
A vers C |
|||
|
Barre BC sur noeud B |
5 - 4 |
B vers C |
T |
12000 |
|
Barre BC sur noeud C |
C vers B |
APPLICATION : PONT MÉTALLIQUE
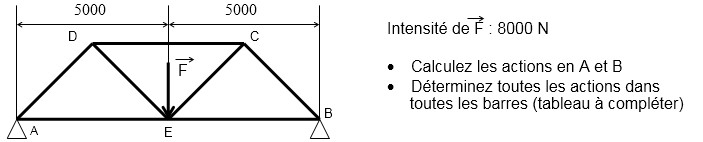
CALCULS : PAR SYMÉTRIE