Enoncé Physique série A 2004
BACCALAUREAT DE L’ENSEIGNEMENT GENERAL – MADAGASCAR
Série : A - SESSION 2004
Epreuve de : Sciences Physiques
Durée : 2 heures 15 minutes
EXERCICE I (7 points)
L’extrémité O d’une corde, de longueur infinie, est animée d’un mouvement vibratoire sinusoïdal, transversal de fréquence N = 20Hz et d’amplitude a = 5cm. La célérité de propagation des ondes le long de la corde est V = 1m/s. A l’instant t = 0s, le point O passe par sa position d’équilibre d’élongation nulle en se déplaçant dans le sens négatif des élongations.
1°)- a) Qu’est-ce qu’une onde transversale ?
b) Définir et calculer :
- la période T
- la longueur d’onde 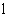 .
.
2°)- Ecrire l’équation horaire du mouvement de O.
3°)- Soient 2 points A et B de la corde tels que OA = 2,5cm et OB = 10cm.
a) Calculer les phases initiales φA et φB de ces 2 points.
b) Comparer les mouvements de A et B.
POUR A2 SEULEMENT :
4°)- Représenter graphiquement l’élongation d’un point M de la corde tel que OM = x = 7,5cm pour O ≤ t ≤ 12,5 . 10 ˉ2s.
EXERCICE II (6 points)
1°)- Faire le schéma du dispositif interférentiel d’Young.
2°)- Les deux fentes fines F1 et F2 sont éclairées par une radiation monochromatique de longueur d’onde 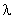 1 = 0,56µm.
1 = 0,56µm.
L’écran d’observation (E) est placé à la distance D = 1,4m du plan contenant les deux fentes F1 et F2.
a) Qu’observe-t-on sur l’écran ?
b) Que peut-on dire de la nature de la lumière ?
3°)- La distance entre les milieux de la 2ème frange obscure située d’un côté de la frange centrale et de la 2ème frange obscure située de l’autre côté de la frange centrale est d = 2,37mm.
a) Calculer la valeur de l’interfrange.
b) En déduire la distance F1F2 = a.
POUR A2 SEULEMENT :
4°)- Les fentes F1 et F2 sont maintenant éclairées par deux radiations monochromatiques de longueurs d’onde respectives 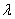 1 = 0,56µm et
1 = 0,56µm et 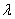 2 = 0,70 µm. Calculer la distance qui sépare deux coïncidences successives des franges brillantes des deux radiations.
2 = 0,70 µm. Calculer la distance qui sépare deux coïncidences successives des franges brillantes des deux radiations.
EXERCICE III (7 points)
1°)- Qu’appelle-t-on :
a) Effet photoélectrique ?
b) Longueur d’onde seuil d’un métal ?
c) Energie d’extraction d’un électron d’un métal ?
2°)- L’énergie d’extraction d’un électron d’une plaque de césium est W0 = 1,8 eV.
a) Calculer la longueur d’onde seuil 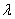 0 de ce métal.
0 de ce métal.
b) On éclaire successivement la plaque par deux radiations de longueur d’onde : 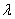 1 = 0,4µm ;
1 = 0,4µm ; 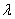 2 = 0,75µm. Les deux radiations permettent-elles l’émission d’électrons par la cathode au césium ? Justifiez votre réponse.
2 = 0,75µm. Les deux radiations permettent-elles l’émission d’électrons par la cathode au césium ? Justifiez votre réponse.
3°)- Lorsque la cellule est éclairée par la radiation de longueur d’onde 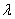 1 = 0,4µm, calculer l’énergie transportée par un photon incident en Joule et en eV.
1 = 0,4µm, calculer l’énergie transportée par un photon incident en Joule et en eV.
POUR A2 SEULEMENT
4°)- a) Calculer en (eV) l’énergie cinétique maximale d’un électron à la sortie de la cathode.
b) Définir et calculer le potentiel d’arrêt.
On donne :
- Constante de Planck : h = 6,62.10 ˉ34J.s
- Charge d’un électron : q = — e = — 1,6 .10 ˉ19C
- Célérité de la lumière dans le vide : C = 3.10 8m.s ˉ1
- 1 eV = 1,6.10 ˉ19J 1 µm = 10 ˉ6m