Série D - Mathématiques

MATHEMATIQUES - Série D - SESSION 1999

 

- - - - - - - - - -

N.B. : Les Quatre Exercices sont obligatoires.

- - - - - - - - -

EXERCICE I(20 points)

Dans le plan complexe P muni d’un repère orthonormé 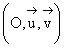d’unité 2cm,

on donne le point A d’affixe –2.

Soit Z le nombre complexe défini par : Z =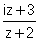, avec z ¹ -2 et z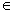C.

On pose Z = X + iY et z = x + iy avec (x, y)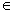IR ² et (X,Y) 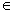IR².

1 -Déterminer X et Y en fonction de x et y.(3 points)

2 -Déterminer et construire dans P les deux ensembles (C) et (D) définis par :

(C ) = { M(x, y) / Z soit réel }.

(D) = { M(x, y) / Z soit imaginaire pur }. (4 points)

3 -Soient B, C et D les points d’affixes respectives : i, 2 + 2i, 1 - i.

On note par S la similitude plane directe qui transforme B en C et C en D.

a -Donner l’expression complexe de S. (3points)

b -Préciser ces éléments géométriques. (6points)

c -Construire l’image du cercle d’équation : x² + y² + 2x - 3y = 0 par S, dans le repère précédent.(4points)

 

 

EXERCICE II(20 points)

 

 

Le tableau ci-dessous donne en milliards de francs malgache (FMG) les importations d’une société, de 1993 à 1998.

 

Année	1993	1994	1995	1996	1997	1998
Rang de l’année : xi	1	2	3	4	5	6
Importations : yi	5	6,5	7	6,5	10	12

1-                 Représenter le nuage de points associé à cette série statistique (x_i, y_i ) dans un repère orthogonal. L’unité graphique sera prise égale à 1cm sur l’axe des abscisses x, et 1cm pour 1 milliards sur l’axe des ordonnées y. (4points)

2-Calculer le coefficient de corrélation linéaire. (6points)

3-Par la méthode des moindres carrés, déterminer une équation de la droite de régression de y en x et représenter cette droite dans le même repère défini ci-dessus. (6points)

4-A l’aide de cette droite de régression de y en x, quelle estimation peut-on faire du montant des importations en l’an 2004 ? (4points)

On exprimera les résultats sous forme décimaux, deux chiffres après virgule.

 

EXERCICE III(20 points)

 

Soit f la fonction définie sur D_f = [ 0 ; 1[ È ] 1 ; + ¥ [ par :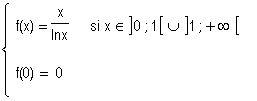  

On note par (C) la courbe représentative de f dans un plan muni d’un repère orthonormé 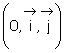d’unité 1cm.

1-                 a)Montrer que f est continue et dérivable au point 0. (3points)

b)Calculer les limites aux bornes de D_f. (2points)

2-                 a)Soit x Î D_f  , calculer f ’(x) et étudier son signe sur D_f.(3 points)

b)Dresser le tableau de variation de f.(1 point )

c)Etudier les branches infinies de la courbe (C).

Tracer (C) et la droite (T) tangente à (C) au point d’abscisse e².(3 points)

3-                 Soit g la fonction définie sur D = ] 1 ; + ¥ [ par : g(x) = 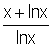,  pour tout x Î D.

On note par (G ) la courbe représentative de g dans le repère précédent.

a)Etudier la position relative de (G ) et (C).(2 points)

b)                 Dresser le tableau de variation de g

et tracer (G ) dans le même repère que (C).(4 points)

c)                 Calculer, en cm², l’aire du domaine plan limité par les deux courbes

(G ), (C) et les droites d’équations respectives x = 2, x = e.(2 points)

On donne ln2 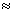0,7 ; e 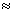2,71 ; e² 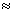7,4 .

 

 

EXERCICE IV(20 points)

 

Soit D₁ un dé cubique truqué numéroté de 1 à 6.

On note p_i la probabilité d’apparition de la face numérotée i lors d’un lancer du dé D₁

( i Î {1, 2, 3, 4, 5, 6} ).

On suppose que p₁, p₃, p₅ forment, dans cet ordre, les trois termes consécutifs d’une suite géométrique de raison 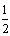 ; puis p₂, p₄, p₆ forment, dans cet ordre, les trois termes consécutifs d’une suite géométrique de raison 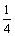et que p₂ = 4p₁.

Soit D₂ un dé cubique non truqué numéroté de 1 à 6.

Chaque face de D₂ a donc la même probabilité d’apparition lors d’un lancer de ce dé.

1-a)Montrer que les probabilités p₁, p₂, p₃, p₄, p₅ et p₆ vérifient le système :

ì p₂ = 4p₁ ; p₄ = p₁

í p₃ =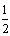p₁  ; p₅ = p₆ =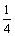p₁ 

î p₁ + p₂ + p₃ + p₄ + p₅ + p₆ = 1. (4 points)

b)Calculer p₁, p₂, p₃, p₄, p₅ et p₆.(6 points)

2-                 On lance les deux dés D₁ et D₂ simultanément. On note par X la variable aléatoire égale à la somme des chiffres obtenus de D₁ et D₂ après lancement.

a)Donner l’univers image de X, (ensemble des valeurs prise par X).(2 points)

b)Calculer la probabilité des événements suivants :

[ X = 2 ] , [ X = 3 ], [ X = 4 ] et [ X ³ 5 ].(8 points)

On donnera les résultats sous forme de fractions irréductibles.