Enoncé Mathématiques série D 2004
MATHEMATIQUES - Série D - SESSION 2004
N.B. : - Les DEUX exercices et le PROBLEME sont obligatoires.
- Machine à calculer autorisée.
EXERCICE 1 (5 points) corrigé
1°) Résoudre dans C l’équation d’inconnue Z . (1pt)
Z 2 – ( 4 + 5 i ) Z – 1 + 7 i = 0.
2°) Le plan complexe (P ) est muni d’un repère orthonormé (O,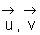
) (unité 1cm). On considère les points A, B et C d’affixes respectives : Z A =1+i ; Z B =3+4i et Z C= 4 –i.
a/ Déterminer l’expression complexe associée à la similitude plane directe S telle que :
S(A) = B et S(B) = C. (1pt)
b/ Préciser les éléments caractéristiques de S. (0,75pt)
3°) On note par I le milieu du segment [ B C ].
a/ Calculer l’affixe ZI de I. (0,25pt)
b/ Placer les points A , B , C et I dans le plan complexe (P ) (0,5pt)
c/ Déterminer et construire l’ensemble ( ) des points M d’affixe Z vérifiant :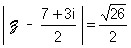 
. (1pt)
d/ Déterminer et construire l’ensemble ( ’ ) image de ( ) par S. (0,5pt)
EXERCICE 2 (5 points) corrigé
Une urne U1 contient six boules : une boule numérotée 0, deux boules numérotées 1 et trois boules numérotées 2.
Une autre urne U2 contient cinq boules : deux boules numérotées 0, une boule numérotée 1 et deux boules numérotées 2.
Les boules sont indiscernables au toucher.
1°) On tire au hasard et simultanément trois boules de l’urne U1.
Calculer les probabilités des événements suivants :
A: << La somme des numéros notés est égale à 4>> (0,5pt)
B: << Parmi les trois boules tirées, deux boules exactement sont numérotées par 2>> (0,5pt)
C: << Le produit des numéros notés sur les trois boules tirées, est différent de 0 >> (0,5pt)
D: << Les trois boules obtenues portent le même numéro >> (0,5pt)
2°) On remet l’urne U1 à sa condition initiale. On tire une boule de l’urne U1 , puis on tire au hasard et simultanément deux boules de l’urne U2. On suppose que les événements élémentaires sont équiprobables. Soit X la variable aléatoire qui, à chaque éventualité, associe le produit des numéros notés sur les trois boules obtenues.
a/ Vérifier que l’univers image de X est égal à l’ensemble { 0 , 2, 4, 8 }. (0,5pt)
b/ Montrer que P (X = 0) =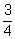 
et P (X > 4) = 
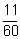. (0,25+0,5pt)
c/ Calculer la probabilité de l’événement : (X = 2). (0,25pt)
d/ Compléter le tableau des valeurs ci-dessous : (0,25+0,25pt)
|
k |
0 |
2 |
4 |
8 |
|
P (X= k) |
|
|
|
|
e/ Montrer que E(X) =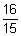 
, E(X) étant l’espérance mathématique de la variable aléatoire X. (0,25pt)
f/ Définir et représenter graphiquement la fonction de répartition F de X.
On utilisera pour la représentation graphique de F un repère orthogonal (O,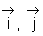
)
(On prendra comme unités : 1cm sur l’axe des abscisses et 6cm sur l’axe des ordonnées) (0,25+0,5pt)
(N.B : On donnera les résultats sous forme de fraction irréductible).
PROBLEME (10 points) corrigé
Soit la fonction numérique f définie sur l’intervalle ] 0, +
[ par : 
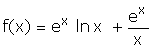
On note par ( C ) sa courbe représentative dans un repère orthonormé (O,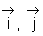) (unité : 2cm).
1°) On donne la fonction numérique g définie sur l’intervalle ] 0, + [ par : 
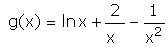
a/ Calculer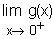 
et 
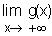. (0,25+0,25)
b/ Pour tout x > 0, calculer g’(x) et étudier son signe. (1+0,5pt)
c/ Dresser le tableau de variation de g. (1pt)
d/ Montrer qu’il existe un et un seul nombre réel α vérifiant g (α) = 0 avec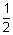 
< α < 1 (1pt)
2°) a/ Pour tout x > 0, calculer f ’ (x). (0,5pt)
b/ Pour tout x > 0, montrer l’égalité f ’(x) =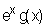 
. (0,5pt)
c/ Calculer f ’ (
). (0,25pt)
d/ Calculer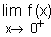 
et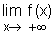 
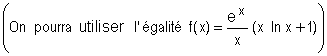. (0,25+0,25)
e/ Dresser le tableau de variation de la fonction f. (0,75pt)
3°) a/ Donner une équation de la tangente (T) à ( C ) au point d’abscisse 1. (0,5pt)
b/ Construire ( C ) et (T) dans un même repère. (1+0,5pt)
4°) On pose pour tout x > 0, h(x) =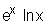 
Montrer que h est une primitive de f sur l’intervalle ] 0, + [. (0,5pt)
5°) Soit I =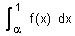 
où α est le réel défini à la question 1°) d/
a/ Montrer que I =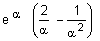 
. (0,5pt)
b/ Interpréter géométriquement l’intégral I. (0,5pt)
On donne ln 2 ~ 0,7 α ~ 0,6 f (α ) ~ 2,1 e ~ 2,7