Enoncé Mathématiques série D 2005
ATHEMATIQUES - Série D - SESSION 2005
N. B : - Le candidat doit traiter les DEUX Exercices et le Problème.
- Machine à calculer autorisée.
EXERCICE 1 (5 points) corrigé
Le plan complexe P est rapporté à un repère orthonormé (O,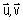 ).
).
On note A le point d’affixe i.
1°) Résoudre dans C l’équation à une inconnue z suivante :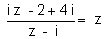 . (1,00pt)
. (1,00pt)
2°) A tout point M d’affixe z, avec z ≠ i, on associe le point M’ d’affixe z’
tel que : z’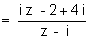 .
.
a/ Exprimer z’ – i en fonction de z. (0,50pt)
b/ Montrer que (z’ – i ) ( z – i ) = – 3 + 4i. (0,25pt)
c/ En déduire la valeur de |z’ – i|.|z – i|. (0,25pt)
d/ Déterminer l’ensemble (C) des points M tels que |z – i| = 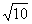 . (0,50pt)
. (0,50pt)
e/ En utilisant les résultats précédents, montrer que si M appartient au cercle de centre A et de rayon 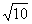 alors M’ appartient à un cercle (C’) de centre A dont on déterminera le rayon. (0,50pt)
alors M’ appartient à un cercle (C’) de centre A dont on déterminera le rayon. (0,50pt)
3°) Soit S la similitude plane directe de centre A, de rapport 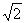 et d’angle de mesure
et d’angle de mesure 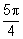 .
.
a/ Ecrire l’expression complexe de S. (1,00pt)
b/ Soit B le point d’affixe 1 + 3i et B’ = S(B). Déterminer l’affixe de B’.
Montrer que B’ appartient au cercle (C). (0,5+0,5pt)
EXERCICE 2 (5 points) corrigé
On dispose de deux dés cubiques parfaits et identiques D1 et D2.
Chaque dé comporte :- trois faces numérotées 1
- deux faces numérotées 2
- une face numérotée 5.
1°/ On lance une fois le dé D1 et on note le numéro apparu sur la face supérieure du dé.
Calculer la probabilité de chacun des événements suivants :
A : « Le numéro apparu est impair ». (0,50pt)
B : « Le dé donne le numéro 1 ». (0,50pt)
2°/ On lance simultanément les deux dés D1 et D2 et on note les numéros apparus sur les faces supérieures des deux dés. On dit qu’on a effectué ainsi ‘‘une épreuve’’.
a) Soit l’événement C : « La somme des numéros notés est égale à 4 ».
Montrer que la probabilité de l’événement C : P(C) = 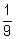 . (0,50pt)
. (0,50pt)
b) Calculer la probabilité de l’événement :
E : « Les deux dés donnent le même numéro ». (0,50pt)
c) Soit X la variable aléatoire réelle qui, à chaque éventualité, associe la somme des numéros apparus sur les faces supérieures des deux dés.
Préciser l’univers image de X puis déterminer la loi de probabilité de X. (0,25+1,0pt)
3°/ Une partie consiste à effectuer 4 épreuves successives d’une manière indépendante.
A chaque épreuve, on note les numéros obtenus. On fait une partie. Soit Y la variable aléatoire réelle égale au nombre de fois de réalisation de l’événement C lors d’une partie.
a) Préciser l’univers image de Y. (0,25pt)
b) Calculer l’espérance E(Y) et la variance V(Y) de Y. (0,50+0,50pt)
c) Calculer P(Y = 3). (0,50pt)
PROBLEME (10 points) corrigé
Soit la fonction numérique f définie sur l’intervalle 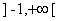 par :
par :
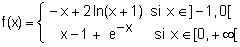 .
.
On note (C) sa représentation graphique dans un repère orthonormé (O,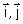 ) (unité : 2cm).
) (unité : 2cm).
1°) a/ Montrer que f est continue en x0 = 0. (0,50pt)
b/ Montrer que 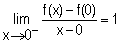 et
et 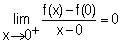 . (0,50+0,50pt)
. (0,50+0,50pt)
Que peut-on en conclure sur f ? (0,25pt)
2°) a / Calculer 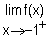 et
et 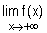 . (0,25+0,25pt)
. (0,25+0,25pt)
b/ si x c ] –1, 0 [, calculer f’(x) et étudier son signe. (0,50+0,25pt)
c/ si x c ] 0, + º [, calculer f’(x) et étudier son signe. (0,50+0,25pt)
d/ Dresser le tableau de variation de f. (1,25pt)
3°) Montrer que la droite (D) d’équation y= x – 1 est asymptote à (C) au voisinage de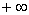 . (0,50pt)
. (0,50pt)
4°) Tracer (C) et (D) dans un même repère (préciser les demi-tangentes à l’origine 0 du repère). (1+0,5+0,5pt)
5°) Soit a un nombre réel tel que a > 1.
On note A(a) l’aire du domaine plan limité par (C), la droite (D) et les droites d’équations respectives x = 1 et x = a.
a/ Exprimer , en cm2, A(a) en fonction de a. (0,50pt)
b/
Calculer .
(0,25pt)
6°) Pour tout nÎIN,
on pose Un = [f(x)
– (x – 1)] dx.
(En remarquant que si nÎIN et xÎ[n, n+1] on a : f(x) = x – 1 + e–x ).
a/ Exprimer Un en fonction de n. (0,50pt)
b/ Montrer que (Un)nÎIN est une suite géométrique dont on précisera la raison et le premier terme. (0,50pt)
7°) Soit g la restriction de f à l’intervalle I =
[0, + ¥[.
a/ Montrer que g admet une fonction réciproque g–1. (0,25pt)
b/ Représenter graphiquement g–1 dans le même repère que (C). (0,50pt)