Enoncé Mathématiques série D 2007
MATHEMATIQUES - Série D – SESSION 2007
NB : - Le candidat doit traiter les DEUX Exercices et le PROBLEME.
- Machine à calculer autorisée.
EXERCICE I (5 points)
Soit le Polynôme P à variable complexe z défini par : P(z) = z3 + (1 + i)z2 + (4 – i)z – 6i + 12.
1- a-Calculer P(– 3i).(0,50 pt)
b-Montrer que l’équation P(z) = 0 admet une solution réelle a que l’on déterminera.(0,50 pt)
c-Déterminer le nombre complexe b tel que P(z) peut s’écrire sous la forme :
P(z) = ( z + 3i ) ( z + 2 ) ( z + b ).(0,50 pt)
d-Résoudre dans C l’équation P(z) = 0(0,75 pt)
2- Dans le plan complexe (P ) muni d’un repère orthonormé (O ;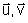 ), on considère les points A, B, C d’affixes respectives zA = – 3i ; zB = – 2 et zC = 1 + 2i.
), on considère les points A, B, C d’affixes respectives zA = – 3i ; zB = – 2 et zC = 1 + 2i.
Déterminer la mesure de l’angle 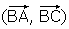 et
et 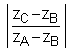 puis en déduire
puis en déduire
la nature du triangle ABC.(0,25+0,25)
3- Soit r la rotation de centre B et d’angle 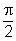 .(0,25 pt)
.(0,25 pt)
Ecrire l’expression complexe de la rotation r.(0,50 pt)
4- On considère la transformation S du plan (P ) dans (P ) qui à tout point M d’affixe z associe le point M’ d’affixe z’ tel que S : z’ = 2iz – 2 + 4i.
a- Donner la nature et les éléments caractéristiques de S.(0,25+0,75)
b- Donner la nature et les éléments caractéristiques de la transformation h telle que r o h = S.(0,50 pt)
EXERCICE II (5 points)
Un sac contient six jetons, portant les lettres A, B, C et D dont la répartition suivant les couleurs est donnée par le tableau ci-dessous :
|
Lettres
Couleurs |
A |
B |
C |
D |
|
Rouges |
0 |
1 |
1 |
0 |
|
Jaunes |
1 |
0 |
0 |
1 |
|
Noires |
1 |
1 |
0 |
0 |
Chaque jeton a la même probabilité d’être tiré.
I-On tire au hasard et successivement sans remise trois jetons du sac.
1) Calculer la probabilité de chacun des événements suivants :
E : ‘‘obtenir exactement un jeton rouge’’.(0,50 pt)
F : ‘‘obtenir dans l’ordre, les lettres B, A, C ’’.(0,50 pt)
2) Soit X la variable aléatoire associée au rang de la première consonne sortie.
a) Déterminer l’univers–image de X.(0,50 pt)
b) Etablir la loi de probabilité de X et calculer l’espérance mathématique E(X) de X.(1+0,25)
II-Une épreuve (E) consiste à tirer simultanément trois jetons du sac.
1) Calculer la probabilité de l’évènement : G : ‘‘obtenir les lettres du mot B A C ’’.(0,50 pt)
2) On répète trois fois de suite et d’une manière indépendante l’épreuve (E).
A chaque épreuve, on marque 1 point si l’événement G est réalisé, sinon on marque 0 point.
Soit Y la variable aléatoire égale au total des points obtenus à l’issue des trois épreuves.
a) Préciser l’univers–image de Y et déterminer la loi de probabilité de Y.(0,50+0,75)
b) Calculer l’espérance mathématique E(Y) de Y puis la variance V(Y) de Y.(0,25+0,25)
PROBLEME (10 points)
On considère la fonction numérique f définie sur IR par : f(x) = (x2 + 1) e–x + x.
On désigne par (C ) la courbe représentative de f dans un repère orthonormé ( O, 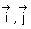 ) d’unité 1cm.
) d’unité 1cm.
I –Soit g la fonction numérique définie sur IR par : g(x) = 1 – (x – 1)2e–x
a) Calculer 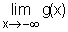 .(0,25 pt)
.(0,25 pt)
b) Montrer que 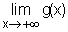 = 1 en admettant que
= 1 en admettant que 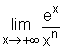 = +¥, nÎ IN.(0,25 pt)
= +¥, nÎ IN.(0,25 pt)
c) Calculer la dérivée g’(x) de g pour tout x Î IR.(0,50 pt)
d) Dresser le tableau de variation de g.(1,00 pt)
e) Calculer g(0) et en déduire le signe de g(x) pour tout x Î IR.(0,25+0,50)
II–1-a)Montrer que 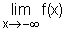 = +¥ et
= +¥ et 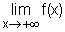 = +¥.(0,50+0,50)
= +¥.(0,50+0,50)
b)Montrer que pour tout x Î IR, f’(x) = g(x) et dresser le tableau de variation de f.(0,50+1,00)
2-a)Montrer que le point A d’abscisse 1 est un point d’inflexion de (C ).(0,50 pt)
b)Donner une équation de la tangente (T) à la courbe (C ) au point A.(0,50 pt)
c)Montrer que la droite (Δ ) d’équation y = x est une asymptote oblique à (C )(0,50 pt)
d)Etudier la branche infinie de (C ) en - ¥ .(0,50 pt)
e)Tracer (T), (Δ ) et (C ).(0,25+0,25+1)
3-a)A l’aide d’une double intégration par parties, calculer l’intégrale : I =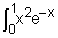 dx.(0,50 pt)
dx.(0,50 pt)
b)En déduire l’aire géométrique A, en cm2, du domaine plan limité par la courbe (C ), la droite (Δ ) et les droites d’équations : x = 0 et x = 1.(0,75 pt)
On donne : 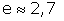 ;
;