Séquence 1: Définition - propriétés

Exercices sur les lois de Descartes- optique

 

 

ex1 : réflexion réfraction:

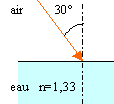
Dessiner le rayon réfléchi et le rayon réfracté et calculer les angles de réflexion et de réfraction

corrigé

angle d'incidence = angle de réflexion =30°

n_air sin 30 = n _eau * sin i₂

sin i₂ = 1*0,5 / 1,33

i₂ = 19,5°

 

Ex 2 : angle limite

 

L'indice d'un verre est est 1,5 .

Quel est la valeur de l'angle limite pour la réfraction verre-air ?

corrigé

 

Lors du passage de l'air dans le verre, le rayon réfracté existe toujours. Par contre lors du passage du verre dans l'air il existe un angle limite d'incidence au dela duquel le rayon réfracté n'existe pas: il y a réflexion totale.

sin( angle limite) = 1/1,5=0,666

41,8°.

 

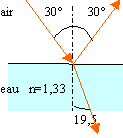
Ex3 :figures à compléter

 

Tracer la marche du rayon lumineux jusqu'à la sortie du prisme d'indice n=1,50, plongé dans l'air dans les deux cas de figure.

 

D'une part, un faisceau perpendiculaire à la surface séparant deux milieux transparents, n'est pas dévié.

D'autre part, le faisceau réfracté existe si l'angle d'incidence est inférieure à i_max tel que sin i_max = 1/n₂ ; sin i_max = 1/1,50 =0,667 soit i_max =42°.

Or l'angle d'incidence vaut 45°, valeur supérieure à i_max : il y a réflexion totale.

 

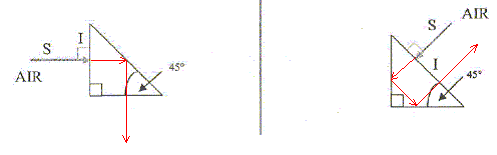
EX 4 :lame à faces parallèles

Un rayon monochromatique arrive sur une vitre faite de verre d'indice n=1,5 et d'une épaisseur e =5 mm. L'angle d'incidence est i =30°.

Calculer l'angle de réfraction du rayon dans le verre puis tracer ce rayon.

Calculer l'angle d'incidence de ce rayon sur le dioptre verre/air.

Avec quel angle de réfraction le rayon émerge t il de la vitre ? Tracer ce rayon émergent.

Comparer la direction du rayon qui arrive sur la vitre et celle de celui qui en sort. Cela dépend il de la valeur de l'indice n ?

Le rayon lumineux incident est de couleur blanche. Comment seront les rayons des différentes couleurs à la sortie de la vitre ? Comparer l'effet d'un prisme et l'effet d'une vitre sur la lumière blanche.

corrigé

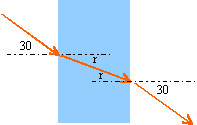
1 sin 30 = 1,5 sin r

sin r = 0,333 d'où r = 19,47°

puis dioptre verre air :

angle d'incidence 19,47 ° (angle alterne interne)

1,5 sin 19,47 = 1 sin i'

i' = 30°

le rayon incident et le rayon émergeant ont des directions parallèles quel que soit l'indice n

donc pas de dispersion de la lumière blanche par la vitre.

Par contre dans un prisme il y a dispersion de la lumière blanche, car la longueur d'onde de la lumière dépend de l'indice n. Le prisme est un milieu dispersif.

Ex5 : prisme 

 

La section du prisme est un triangle équilatéral

 

 

 

L'indice de réfraction du prisme est 1,5. Dessiner les rayons obtenus par réfraction sur les 2 faces AB et AC et calculer l'angle du rayon émergent avec la normale à la face AC.

 

corrigé

 

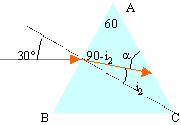
sin(30)=1,5 sin(i₂) d'où i₂= 19,5° et a=49,5°

 

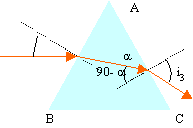
1,5 sin(90-49,5)= sin(i₃) d'où i₃= 77°