Exercices bac TA sur les ondes
Corrections avec
rappel du sujet
sujet1 sujet2
Sujet n°1

Correction :
1°/a-On observe
une onde progressive sinusoïdale.
b- La pulsation w du mouvement sinusoïdal de l’extrémité de
la lame est reliée à la fréquence N par la relation : w=2.p.N =40.p, d'où :
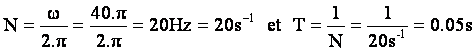
2°/ La longueur
d’onde l est la longueur parcourue par l’onde progressive pendant une période
T.
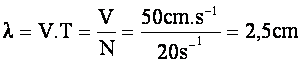
3°/ Le point M
situé à la distance d =5cm (soit 2l) de la source, reçoit l’onde avec un retard t
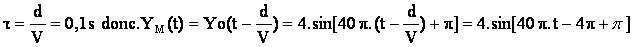 .
.
M vibre en retard
de phase de 4p par rapport à la
source ce qui revient à dire que lorsque l’onde a atteint le point M, les deux
points M et O vibrent en phase.
(en effet à la même date t les
fonctions sinus de Yo et YM auront la même valeur)
4°/ A t=0.05s=T,
la lame a effectué une oscillation et l’onde s’est propagée d’une longueur
d’onde l soit 2,5 cm.
La courbe
ci-dessous représente le mouvement de la source O en fonction du temps. Elle
montre que la lame commence son mouvement en descendant.
(graphique non demandé)
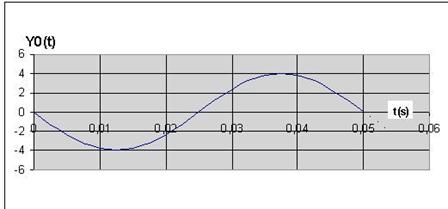
Mouvement de la source en fonction du temps
Le front de l’onde
est donc un creux suivi d’une bosse
comme l’indique la figure ci-dessous. A t=0.05s l’onde a parcouru la moitié de
la distance OM.
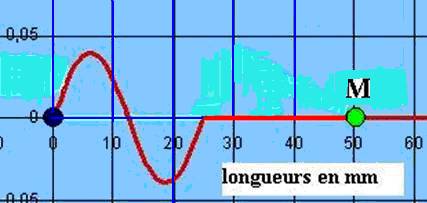
Aspect de la surface de l’eau à t=0.05s
Sujet n° 2

1° a/une onde est transversale si la direction de la perturbation
est perpendiculaire à la direction de propagation.
b/ la période T est la durée
d’une oscillation complète des points du milieu.
Sa valeur est T=1/20=0,05s=50ms
La longueur d’onde l est la distance parcourue par l’onde
pendant la durée d’une période T.
Sa valeur est l=V.T=1.0.05=0,05m=5cm
2° Equation horaire du point source O :
L’équation est du type :
Yo(t)= a.sin[(2.p/T).t+fo]
L’amplitude a= 0,05m ;
T=1/20=0,05s ; 2p/T=w=40.p
La phase à l’origine dépend des conditions initiales.
A t=0, Yo=0 soit sinf=0.Ceci implique que fo=0 ou p (à 2kp prés).
La vitesse transversale du point O est vo= dY/dt=aw.cos[w.t+f]
.Elle est négative à t=0 puisque O se déplace vers les Y <0 donc cosf<0 et fo=p.
L’équation est finalement :
Y(t)=
0,05. sin[(2.p/T)t+p]= 0,05. sin[40.p.t+p]=
- 0,05.sin[40.p.t]
3°/a-La
vibration en A est en retard sur celle de O de tA=xA/V=2,5.10-2/1=25.10-3s=25ms(soit
une demi- période).
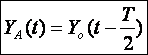
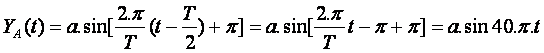
La phase initiale est donc fA=0, ce qui
signifie que la vibration en A possède un retard de phase de p sur la vibration en O. A est O vibrent en opposition de phase.
La vibration en B est en retard sur celle de O de :
tB=xB/V=10.10-2/1=10-1s=100ms(soit
2T), par conséquent :
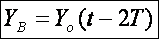
Soit :
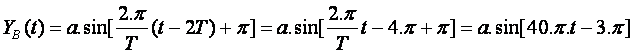 ]
]
La phase fB=-3p , ce qui signifie que B possède un retard
de phase de
p-(-3p)=4p sur O (nombre
pair de p).
B et O vibrent donc en phase (pour t>50ms)
b- Le retard de phase de B sur A est fA-fB=0-(-3p) =3p (nombre impair de p).
B et A vibrent en opposition.
4°/ graphe de la vibration
en M (en rouge)au cours du temps :
La vibration commence à la date t=xM/V =7,5.10-2s=75ms=1,5T
M est situé à 1,5l de O, ce
point vibre donc en opposition de phase par rapport à O.
Le point commence à se déplacer dans le sens négatif des
élongations.
(sur le graphe on a représenté en vert l’élongation du point source
O au cours du temps)