Le mouvement rétrograde de Mars
Avertissement : ce document peut être
utilisé au moins partiellement dans toutes les classes de lycée.Les lois de
Képler et la partie mathématique du dernier paragraphe sont du niveau exclusif
de terminale.
I- Objectifs du document :
-découvrir quelques éléments d’histoire des sciences
-approfondir les notions de référentiel et de relativité du mouvement. (notions exigibles en classe de seconde)
-définir les référentiels héliocentrique et géocentrique. ( indispensables pour l’étude des satellites en terminale)
-utiliser un logiciel de pointage avec calque virtuel pour tracer une trajectoire dans deux référentiels différents.
-vérifier la troisième loi de Képler.
-établir les équations géocentriques du mouvement d’une planète.(complément mathématique du niveau de terminale)
-utiliser les résultats précédents pour tracer les trajectoires dans un tableur.
II-Observation de la trajectoire de Mars depuis
Le document ci-dessous représente les positions successives de Mars parmi les constellations de juillet à octobre 2005. La planète se déplace de la gauche vers la droite, puis change de sens pour repartir ensuite vers la droite…La trajectoire trace une boucle caractéristique très aplatie que l’on nomme rétrogradation.
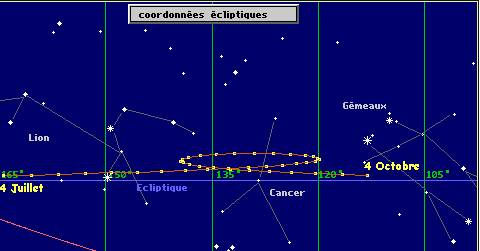
Comment expliquer cette rétrogradation de Mars ?
Plusieurs interprétations de celle-ci furent proposées en relation avec les modèles de l’Univers qui évoluèrent au cours des siècles. Nous allons présenter les modèles de Ptolémée et de Képler.
Pour faciliter la compréhension de ces derniers nous proposons au lecteur d’effectuer le tracé de la trajectoire de Mars dans les référentiels héliocentrique puis géocentrique avec le logiciel Avistep.
Le lecteur intéressé pourra aborder l’étude mathématique.

III- L’interprétation de Ptolémée (IIème siècle ap. JC):
le géocentrisme
Elle est basée sur les deux principes suivants :
-le géocentrisme : toutes les planètes du système solaire, y
compris le Soleil se meuvent autour de
-le mouvement des planètes
résulte d’une combinaison de mouvements
circulaires et uniformes.
Comment expliquer cette rétrogradation en respectant ces deux principes ?
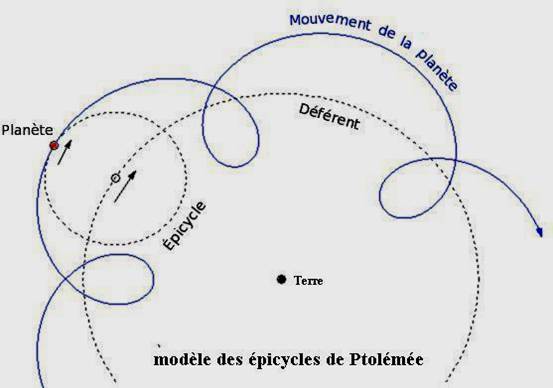
Ptolémée propose le système des épicycles :
Dans ce système, les planètes se
meuvent sur des petits cercles appelés « épicycles » qui tournent sur
eux-mêmes d’un mouvement uniforme…Les petits cercles sont eux-mêmes entrainés sur
un cercle plus grand « le déférent » centré sur
Le cercle déférent de chaque
planète tournant autour de
Ce modèle très imparfait permettait
cependant d’accorder les observations avec les idées religieuses et
philosophiques de l’époque qui attribuaient à
IV- L’interprétation de Képler (1605) :
l’héliocentrisme :
Kepler exploite les mesures précises effectuées pendant une trentaine d’années par son maître Tycho Brahé (astronome danois) .Contrairement à son maître, il réfute le modèle géocentrique et reprend les hypothèses de Copernic qui place le Soleil en position centrale, toutes les planètes tournant autour de lui.
Selon ce modèle,
L’exploitation des mesures de Tycho Brahé obligèrent Képler à abandonner la trajectoire circulaire et le mouvement uniforme et à énoncer les 3 lois suivantes :
1ère loi : les planètes décrivent des ellipses dont l’un des foyers est occupé par l’astre central.
2éme loi : les aires balayées par le rayon vecteur de l’astre sont proportionnelles au temps.
(loi des aires)
3éme loi : le carré des périodes T des astres d’un même système est proportionnel au cube du demi grand axe r de l’ellipse.(loi dite des périodes)

Cette relation établie par Képler empiriquement fut démontrée ultérieurement par Newton à partir de sa deuxième loi de la dynamique.
Ces lois s’appliquent à tous les systèmes : système du Soleil avec ses planètes, système de Jupiter avec ses satellites, système d’Uranus ..etc..
Enfin, Képler entreprit de
résoudre l’énigme de la rétrogradation de Mars. Celle-ci n’est en fait qu’un
mouvement apparent vu de

Pour approfondir cette question, cliquer sur le lien :
Animation sur les
lois de Képler
V- Définition des référentiels héliocentrique et géocentrique :

Observons le schéma ci-dessous.
Par commodité chaque référentiel a été représenté par un repère cartésien particulier qui lui est lié. Convenons de le nommer « repère associé ».
Le repère associé au référentiel héliocentrique (H) a pour origine le centre du Soleil et ses 3 axes sont orientés vers des étoiles a, b et c lointaines (considérées fixes).
Signalons que le Soleil tourne sur lui-même et qu’il possède donc un mouvement de rotation propre par rapport à ce référentiel
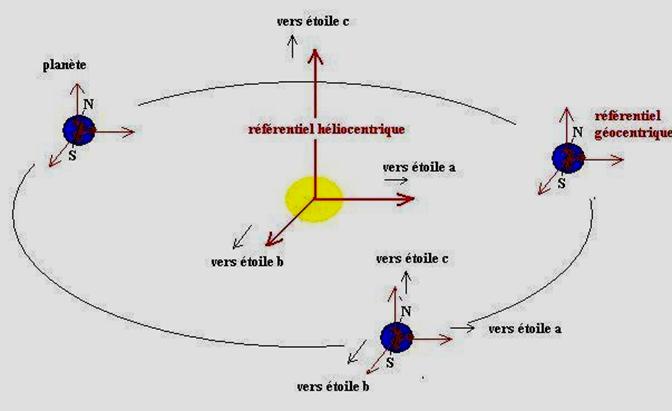
Un référentiel géocentrique (G) peut être défini pour toute planète.
Le repère associé choisi a pour origine le
centre de la planète (ici c’est
La trace elliptique appartient au
plan de l’écliptique. Les centres des planètes du système solaire
évoluent quasiment tous dans ce plan.
L’axe nord-sud de
VI-Tracé des trajectoires héliocentrique et géocentrique de
Mars avec le logiciel « Avistep » (TP) :

Dans le « dossier vidéo » de la médiathèque, ouvrir « Avistep » et charger le dessin animé «17 trajectoire Mars.avi » .
Remarque: ayant ouvert le logiciel, il est nécessaire de revenir au texte du TP pour suivre le protocole
proposé . Et vice versa.
Il suffit pour cela de mettre en
réduction la page ouverte du logiciel .
En cliquant dans la barre des
taches (en bas de l’écran) sur le document ouvert réduit, on peut réaliser des « allers et retours » entre le
texte et le logiciel .
Le travail proposé peut s’effectuer en deux étapes.
1-Tracés des trajectoires héliocentriques de
Le plan du tracé des trajectoires est celui de l’écliptique.
Dans le fichier
« Mesures » indiquer « deux
marques par image » afin de pouvoir donner simultanément la position
des centres de
Tracer un repère centré sur le Soleil(S). Démarrer la lecture du film à la 1ère image (date 0).Cliquer sur les centres des planètes(T) puis (M), le film avance d’une image et la nouvelle date s’affiche en bas à gauche.
Evaluer la période de Mars en jours terrestres puis en années terrestres.
Sachant que la distance moyenne Soleil-Mars est de 1,5 U.A ,montrer que la planète Mars vérifie la 3ème loi de Képler (loi des périodes).
On précise que la distance Soleil-Terre est égale par convention à 1 U.A (une unité astronomique).
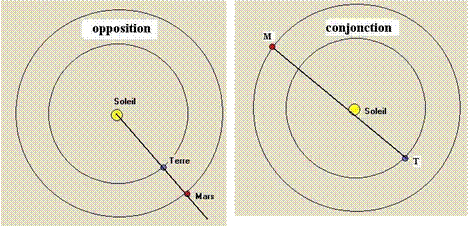
On peut repérer la date d’opposition (date pour laquelle S.T.M sont alignés avec T entre S et M) et la date de conjonction (S.T.M alignés avec S entre T et M).
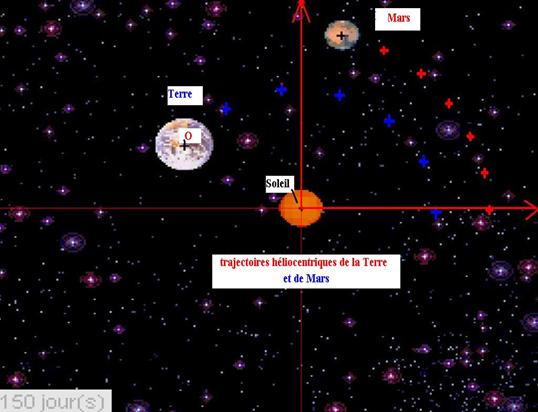
Lors de son opposition,
Mars est au plus prés de
2- Tracé de la trajectoire de Mars par rapport au
référentiel géocentrique de
Il faut faire apparaître le calque virtuel sur l’écran. Cliquer sur le logo correspondant dans la barre des taches inférieure.
Remettre le film à la 1ère
image(date t=0). Déplacer le calque et faire coïncider l’intersection des deux
axes avec le centre de
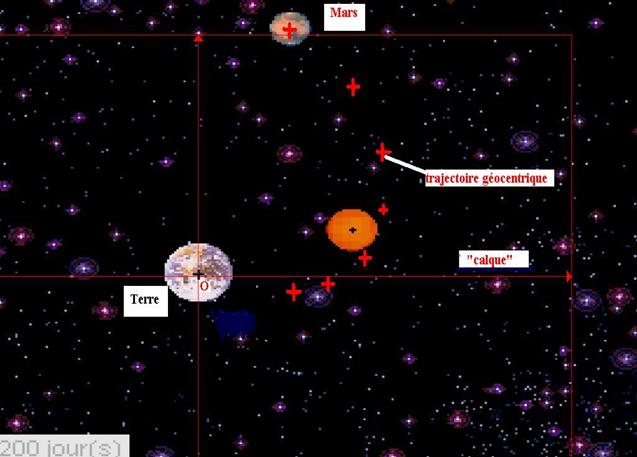
Nous obtenons la boucle caractéristique de la rétrogradation vue par un observateur qui serait placé selon une direction perpendiculaire au plan de l’écliptique et à une grande distance de ce dernier.
Vue de
Au sommet de la boucle, Mars
est au plus prés de
Au contraire, lorsque la distance entre Mars et
Evaluer la durée entre deux rétrogradations successives de Mars.
VII -Coordonnées géocentriques d’une planète (niveau terminale):

Nous proposons d’établir celles-ci pour toute planète P du système solaire.
Hypothèse simplificatrice :
La période de
A la date t
l’élongation angulaire de
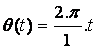
A la même date t , l’élongation de la planète par rapport à (H )est :
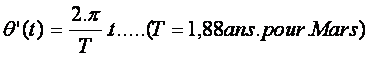
.
La distance terre soleil ST =1U.A et la distance SP=k (k=1.5 pour Mars)


Pour tracer les trajectoires de Vénus, Mars et Jupiter en utilisant les équations précédentes, cliquer sur le lien ci-dessous :
Trajectoires
géocentriques (animations)