Mouvement d’une balle de tennis dans le champ de pesanteur
I -Objectifs :
Rechercher un modèle mathématique du mouvement d’une balle
de tennis (voir photo ci-dessous).

Hypothèse :peut-on considérer que la seule force
responsable de celui-ci est le poids de l’objet ce qui revient a assimiler le
mouvement à une « chute libre » (ici avec vitesse initiale de
direction non verticale). Quel serait l’écart entre ce modèle et les résultats
expérimentaux.
Quelles sont les autres forces pouvant intervenir ? Peut-on
toujours les négliger devant le poids?
II-Connaissances
requises :
Cinématique :
-Mouvements rectiligne uniforme et uniformément varié.
-Construction des vecteurs vitesse et accélération en un
point de la trajectoire.
Dynamique :
-Les lois de Newton et leur exploitation dans le but
d’établir les équations paramétriques du mouvement.
III- Détermination du vecteur accélération en un point :
1-méthode graphique de détermination :
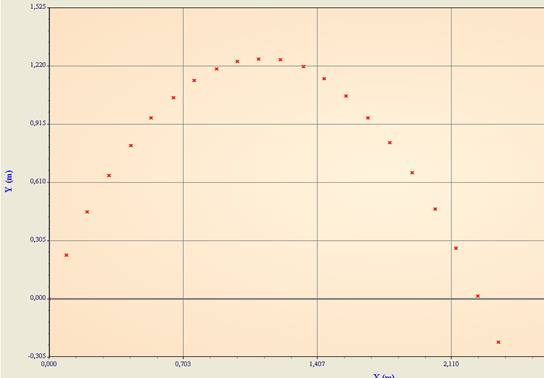
-Le document ci-dessous donne les positions successives du
mouvement du centre d’inertie d’une balle de tennis. Le tracé est obtenu à
partir du clip vidéo : « parabole tennis ».
-Faire une copie d’écran agrandie de ce
document et l’imprimer pour pouvoir travailler dessus : l’intervalle de
temps entre 2 positions successives est : dt =0.05s
-Déterminer l’échelle des distances du document sachant que la
distance réelle entre 2 traits de graduation est de 0,305m,
-Choisir un point pour le
tracé ; L’auteur a choisi le point d’altitude maximum (point
5 dans les constructions). Il est intéressant que les groupes d’élèves ne
choisissent pas tous les mêmes points,
cela permettra de voir l’évolution
éventuelle de l’accélération au cours du mouvement.
Question : après obtention de plusieurs tracés, proposer une
expression du vecteur accélération. Que peut-on dire de ce vecteur au cours du
mouvement ?
- Pour revoir les méthodes de tracé de ce vecteur :
point méthode :tracé du vecteur accélération
Correction
-

Tracé obtenu après
agrandissement
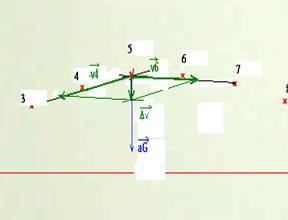
Evaluons les valeurs des vitesses aux 2 points qui encadrent
le point 5.
V4=A3A5/ 2.dt= 2,32m.s-1.
V6=A5A7/2.dt= 2.31m.s-1.
Construire les vecteurs V6
et –V4 en choisissant le point A5 comme
origine commune et en respectant l’échelle des vitesses: 1cm <->1m.s-1.
Tracer le vecteur variation
de vitesse entre A4 et A6, soit 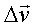 .
.
La longueur de ce vecteur est de 1cm soit :
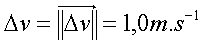
Et comme :
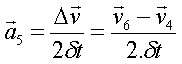
La valeur approchée de l’accélération est :
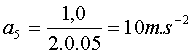
Et la construction semble monter que sa direction est verticale.
D’autres mesures montreront
que le vecteur accélération a même valeur et même direction en tous les
points (aux incertitudes de mesures prés).
Il semble possible d’en déduire que :
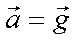
Ce qui rend
l’hypothèse d’une chute « libre »vraissemblable
b-étude du mouvement
de la balle avec le logiciel Avistep.

Cliquer sur le lien
suivant Dossier vidéo
Dans le dossier vidéo, lire le clip
vidéo : « parabole tennis » avec Avistep
(L’échelle du document est donnée par l’image ci-dessus)
Tracés à déterminer :
Pointer les positions successives de la balle et demander le
vecteur accélération de chaque point.
On demandera
également les tracés en fonction du temps des grandeurs suivantes :
-Projection horizontale de la vitesse vx(t).
-Projection verticale de la vitesse vy(t)

Question :
Les documents obtenus
permettent-ils de conclure sur la validité du modèle de la chute libre ? Justifier
la réponse.
Correction

Le graphique ci-dessous confirme
que le vecteur accélération est constant et que sa valeur est proche de 9,8m.s-2.Le
modèle de la chute libre semble très satisfaisant
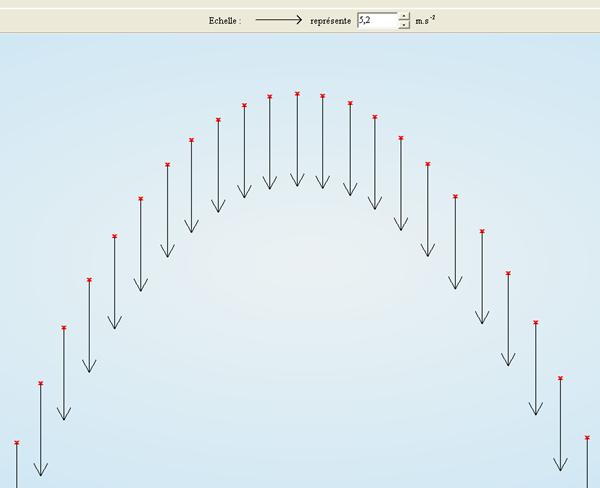

.
Les projections des vitesses :
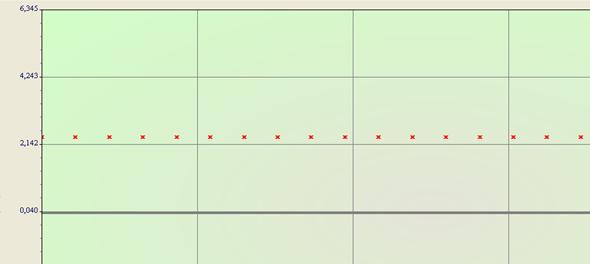

Vx
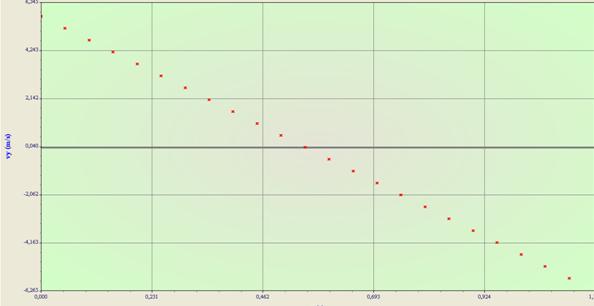

Vy
Résultats :
Vx est constant au cours du mouvement.
Vy est une fonction affine
décroissante de t.
Conclusion :
Le mouvement de la balle résulte de la
composition d’un mouvement rectiligne uniforme horizontal et d’un mouvement
rectiligne vertical uniformément
varié.
Ceci est en accord avec les deux
lois de Newton de la dynamique et confirme un peu plus l’hypothèse d’une
« chute libre ».
-selon une direction horizontale la
balle n’est soumise à aucune force (si l’on néglige les frottements !) et
la 1ére loi (ou principe d’inertie) s’applique,
le mouvement projeté sur Ox est rectiligne et uniforme.
-selon une direction verticale, la
balle est soumise à une force constante :
le poids et la 2éme loi s’applique, le mouvement projeté sur Oy est
rectiligne et uniformément varié (accéléré dans la phase
descendante et décéléré dans la phase montante).
II Etude théorique du
modèle de la chute libre :

a-équations paramétriques du mouvement :
Le système étudié est la balle, de centre d’inertie G.
Nous supposerons que la seule force appliquée est le poids P.
Le référentiel d’étude est la Terre, considéré galiléen.
Nous pouvons appliquer la 2ème loi de Newton.
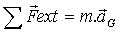 =>
=> 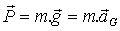 =>
=> 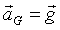
Ce qui confirme la
construction précédente de l’accélération.
Fixons les conditions initiales du mouvement :à t=0,la
balle est lancée au point origine O avec une vitesse vo qui fait un angle a
avec l’horizontale.
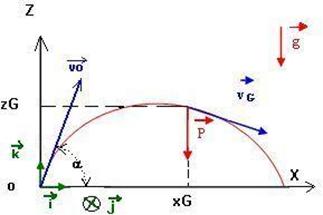
Choisissons un repère Oxyz lié au référentiel terrestre
comme l’indique la figure ci-dessous.
-le vecteur
unitaire k est vertical ascendant ;
-le plan (i,k) contient le vecteur vitesse
initial vo.
-l’origine O coïncide ave la position de la balle à
l’instant où la balle quitte la main .
Dans ce repère et à la date t=0, nous avons :
|
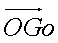
|
xo=0
yo=0
zo=0
|
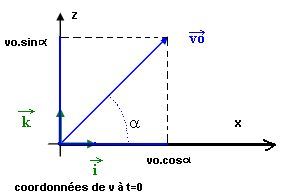
A une date t quelconque, G a pour coordonnées (x,y,z) ,sa
vitesse : 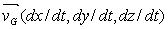
Et son accélération : 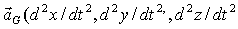 )
)
|
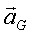
|
d2x/dt2=0
d2y/dt2=0
d2z/dt2=-g
|
Les coordonnées du vecteur
vitesse sont des primitives des
coordonnées du vecteur accélération. Compte tenu des conditions initiales, nous
obtenons ;
|
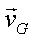
|
dx/dt=vo.cosa
dy/dt=0
dz/dt=-gt
+ vo.sina
|
Les coordonnées du vecteur
position OG sont des primitives des
coordonnées du vecteur vitesse. Compte tenu des conditions initiales, nous
obtenons les équations paramétriques :
|
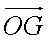
|
x(t)=(vo.cosa).t+
xo = (vo.cosa).t
y(t)=yo=0
z(t)=-1/2.g.t2 + (vo.sina).t + zo= -1/2gt2+(vo.sina).t
|
Nous déduisons de ces équations
les résultats :
y(t)=0,la trajectoire du centre
d’inertie G est dans le plan vertical
xOz contenant le vecteur vitesse initial vo.
x(t)=vo.cos a t : le mouvement de la projection de G sur l’axe horizontal est uniforme.
z(t)=-1/2.g.t2 + vo.sina.t :
le mouvement de la projection de G sur
l’axe vertical Oz est uniformément varié.
Résultats vérifiés par l’étude
expérimentale précédente.
b-Equation de la trajectoire :
On établit l’équation de la
trajectoire en éliminant t entre les
équations paramétriques.

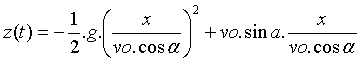
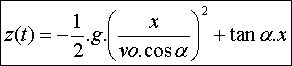
La trajectoire est une portion de
parabole située dans le plan vertical contenant vo.
En posant z=o, la racine de
l’équation donne la portée du tir soit xmax=sin2a.vo2/g
Application numérique :le
tableau de mesure du logiciel donne les conditions initiales
ao=65,6°
et vo=5,42m.s-1 ce qui donne :
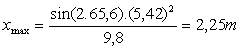
La valeur expérimentale lue sur
le graphique est très voisine de 2.2m .L’écart avec la valeur théorique est
infime. L’hypothèse de la chute libre est très
satisfaisant.
III Le modèle de la chute libre est-il toujours satisfaisant ?
1-Autres forces pouvant intervenir :
Le mouvement s’effectuant dans l’air, il faut
ajouter au poids:
-une force de frottement :
Son calcul est complexe car il faut prendre en
compte du coefficient de pénétration
dans l’air ! Le modèle du frottement fluide proportionnel au carré de
la vitesse est le plus probable .
-la poussée d’Archimède.
-la force de Magnus. Celle-ci est bien connue des joueurs de
football, elle résulte d’une rotation de la balle sur elle même .Elle donne
« de l’effet » latéral à la balle.
Dans ce cas le mouvement n’est
plus plan.
2-simulation du mouvement :
Vous pouvez, à titre
documentaire, réaliser une simulation en
prenant en compte : le poids , la force de frottement fluide, la poussée d’Archimède. Il faudra donc
considérer que la balle ne tourne pas sur elle-même. On pourra comparer son
mouvement dans l’air à celui dans le vide et apprécier les écarts sur la
trajectoire, la vitesse, l’accélération… On vérifiera par exemple que
l’hypothèse de la chute libre est de moins en moins satisfaisante pour des vitesses de plus en plus grandes et
une masse plus faible…

Mouvement d'un projectile dans le champ de
pesanteur(animation)
Résultats de l’étude
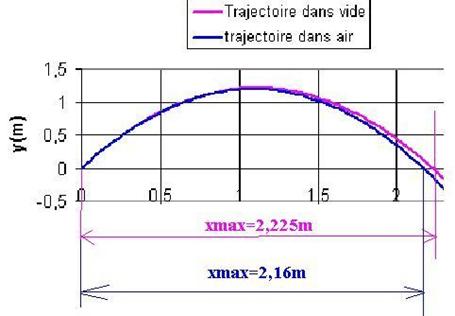
L’écart relatif entre la portée dans l’air et celle
dans le vide est : (2,225-2,16)/2,225=0,029( environ 3%)
Le modèle de la chute libre est très satisfaisant.
